Треугольник Паскаля.Связь треугольника Паскаля с арифметическими прогрессиями.
Треугольник Паскаля
Связь треугольника Паскаля с
арифметическими прогрессиями
Треугольником Паскаля называется бесконечная треугольная
таблица, в которой на вершине и по боковым сторонам стоят единицы, каждое из
остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей
строке.
Свойства треугольника
Паскаля
- Сумма
чисел -ной строки (отсчет ведется с нуля) треугольника Паскаля
равна . Действительно, при переходе от каждой строки к следующей
сумма членов удваивается, а для нулевой строки она равна .
- Все
строки треугольника Паскаля симметричны. Потому что при переходе от каждой
строки к следующей свойство симметричности сохраняется, а нулевая строка
симметрична.
- Каждое
число в треугольнике Паскаля равно , где — номер строки, —
номер (отсчет ведется с нуля) элемента в строке.
- Каждое
число треугольника Паскаля, уменьшенное на единицу, равно сумме всех
чисел, заполняющих параллелограмм, ограниченный диагоналями, на
пересечении которых находится этот элемент.
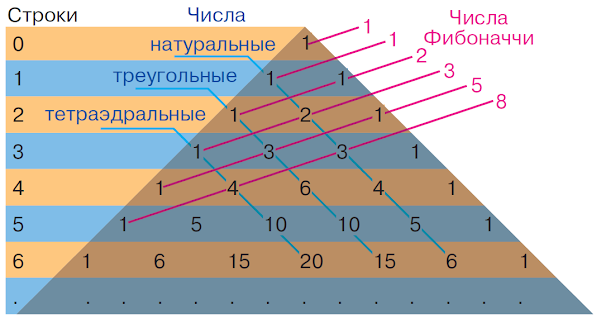
- Вдоль
диагоналей, параллельных сторонам треугольника, выстроены треугольные
числа, тетраэдрические числа и т.д.
- Если
посчитать для каждой восходящей диагонали треугольника Паскаля сумму всех
стоящих на этой диагонали чисел, то получится соответствующее число
Фибоначчи.
- Числа треугольника симметричны (равны)
относительно вертикальной оси.
- В строке с номером n (нумерация
начинается с 0):
- первое и последнее числа равны 1;
- второе и предпоследнее числа равны n;
- третье число равно треугольному числу , что
также равно сумме номеров предшествующих строк;
- четвёртое число является тетраэдрическим;
Треугольными числами называется количество
шаров, которые можно выложить в виде равностороннего треугольника.
Тетраэдрическими числами называется количество
шаров, которые можно выложить в виде правильного тетраэдра.
Последовательность , при называется последовательностью
Фибоначчи, а ее члены — числами Фибоначчи.
Арифметические прогрессии высших порядков 2.0
Казалось бы,
арифметические прогрессии — тема девятого класса, что тут можно дванолить? А
вот нет. Сегодня мы делаем максимальный упор на прогрессии высших порядков. И
это одновременно и просто, и нихуя не просто.
Итак,
напоминаю,
1 5 9 13 17 21… — арифметическая прогрессия первого порядка, потому что
5-1 = 9-5 = 13-9…
1 5 10 16 23
31… — арифметическая прогрессия второго порядка, потому что
31-23 = 23-16+1 = 16-10+2 = 10-5+3…
То есть,
разности прогрессии второго порядка образую прогрессию первого порядка:
4 5 6 7 8
Аналогично
можно ввести более высокие прогрессии — третьего порядка — её разности образуют
прогрессию второго порядка, четвёртого порядка — её разности образуют
прогрессию третьего порядка, и любую другую прогрессию.
И ещё введём
прогрессию нулевого порядка:
7 7 7 7 7…
И
последовательность нулей:
0 0 0 0 0…
Назовём её
архипрогрессией.
Самым
знаменитым примером прогрессий высших порядков являются последовательности
степеней. Например,
1 2 3 4 5 — прогрессия первого порядка
1 4 9 16 25 — прогрессия второго порядка
1 8 27 64 125 — прогрессия третьего порядка
Вы легко можете
это проверить. Вообще, арифметические прогрессии очень близки степеням.
Последовательность разностей прогрессии сродни производной таких функций.
Давайте возьмём
прогрессию третьего порядка:
1 5 12 24…
Что нам нужно
для того, чтобы найти её последующие члены? В первую очередь, нужно всё-таки
знать, что это прогрессия третьего порядка. Мы знаем, потому что я это сказал.
Но если
обобщать: нужно знать порядок прогрессии.
На основе
данных нам четырёх членов, мы можем составить последовательности разностей. Вот
так:
1 5 12 24
4 7 12
3 5
2
Раз мы знаем,
что это прогрессия третьего порядка, то делаем вывод, что в последней строке у
нас прогрессия нулевого порядка — последовательность двоек. Эту
последовательность мы можем продолжить вправо:
2 2 2 2 2
Предпоследняя
строка — прогрессия первого порядка с разностью 2 и с первым членом 3. Значит,
любой другой член будет больше предыдущего на 2:
3 5 7 9 11 13
2 2 2 2 2
На основе этой
прогрессии мы можем продолжить вторую строку вправо.
4 7 12 19 28 39
52
3 5 7 . 9 . 11 13
2 2 2 . 2 . 2
Точки я
поставил просто чтобы выровнять таблицу. Обратите внимание: каждое последующее
число равно сумме предыдущего с числом под ним. Это справедливо для всех строк.
Используя полученную нам прогрессию, можем продолжить первоначальную до
восьмого члена:
1 5 12 24 43 71
110 162
4 7 12 19 28 39 52
3 5 7 . 9 . 11 13
2 2 2 . 2 . 2
Продолжая наши
последовательности тем же образом, получим ещё больше членов. Тут же все любят
члены, да?
Но давайте
подумаем, что нам действительно нужно знать, чтобы строить вот такие вот
таблички.
Мы
отталкивались от последней строки, а в последней строке у нас было только одно
число — 2. Значит, нам нужно знать первый член последней строки.
В предпоследней
строке мы просто прибавляли везде 2, но с самого начала у нас было 3 — которое
к 2 никак не относится. Значит, мы должны знать первый член предпоследней
строки.
Аналогично
придём к выводу, что нам нужно знать первые члены всех остальных строк. И
больше ничего. То есть, чтобы строить таблицу, нам достаточно знать всего 4
числа.
Все числа в
красной рамочке — побочные. Зачем мы их ищем — непонятно. Но других методов мы
не знаем. Ведь так?
Теперь давайте
заметим, что n-й член в строке равен сумме первого члена в этой строке со всеми
членами строки ниже вплоть до (n-1)-го члена. Например,
24 = 1 + 4+7+12
А мы знаем
формулу суммы прогрессии первого порядка.
Значит, n-й
член прогрессии второго порядка равен
Треугольник
Паскаля целиком состоит из арифметических прогрессий, посмотрите, например, на
зелёную линию.





Комментарии
Отправить комментарий