Типы арифметических прогрессий.

 

Типы арифметических прогрессий

1. Арифметическая прогрессия — это монотонная последовательность, которая состоит из ряда чисел. В этом ряду каждое последующее число есть результат добавления к предыдущему одного и того же числа d.

Например: 2; 4; 6; 8; 10…..

2. Арифметической прогрессией второго порядка называется такая последовательность чисел, что последовательность их разностей сама образует простую арифметическую прогрессию. Примером может служить последовательность квадратов натуральных чисел:

1, 4, 9, 16, 25, 36, …

разности которых образуют простую арифметическую прогрессию с разностью 2:

3, 5, 7, 9, 11, …

 

3. Характер этих упорядоченных последовательностей чисел во многом определяется знаком числа d. Выделяют следующие виды алгебраических прогрессий:

·        возрастающая, когда d положительное (d>0);

·        Пример: 3, 5, 7, 9, 11…(d =2).

·        постоянная, когда d = 0;или стационарная

·        Пример: 4, 4, 4, 4, 4, 4…(d=0).

·        убывающая, когда d отрицательное (d<0).

·        Примеры: 20, 10, 0, -10, … (d = -10)

·                            10, 5, 0, -5, -10, -15… ( d = -5)

·         

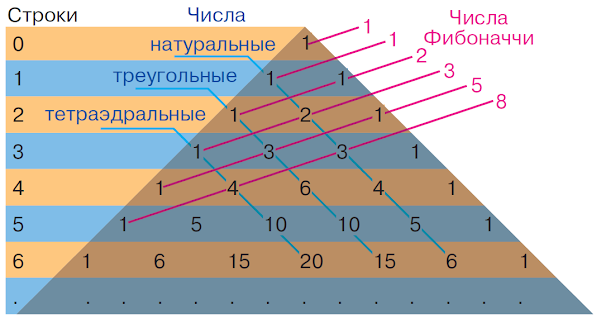
Треугольное число — один из классов фигурных многоугольных чисел, определяемый как число точек, которые могут быть расставлены в форме правильного треугольника.

Треугольные числа {\displaystyle 1,3,6,10,15,\ldots }  также образуют арифметическую прогрессию второго порядка, их разности образуют простую арифметическую прогрессию.

Фигу́рные чи́сла — числа, которые можно представить с помощью геометрических фигур. Это историческое понятие восходит к пифагорейцам, которые развивали алгебру на геометрической основе и представляли любое положительное целое число в виде набора точек на плоскости. Отголоском этого подхода остались выражения «возвести число в квадрат» или «в куб»

Тетраэдральные числа {\displaystyle 1,4,10,20,35,\ldots }  образуют арифметическую прогрессию третьего порядка, их разности являются треугольными числами.

Аналогично определяются и прогрессии более высоких порядков. В частности, последовательность n-ных степеней образует арифметическую прогрессию n-го порядка.

 

Традиционно различают два основных класса фигурных чисел

·        Плоские многоугольные числа — числа, связанные с определённым многоугольником. Они делятся на классические и центрированные.

·        Пространственные многогранные числа — числа, связанные с определённым многогранником

 

В свою очередь, каждый класс фигурных чисел делится на разновидности, каждая из которых связана с определённой геометрической фигурой: треугольником, квадратом, тетраэдром и т. д.

Существуют также обобщения фигурных чисел на многомерные пространства. В древности, когда арифметика не отделялась от геометрии, рассматривались ещё несколько видов фигурных чисел, в настоящее время не используемых

Виды фигурных чисел

 

Фигу́рные чи́сла — числа, которые можно представить с помощью геометрических фигур. Это историческое понятие восходит к пифагорейцам, которые развивали алгебру на геометрической основе и представляли любое положительное целое число в виде набора точек на плоскости. Отголоском этого подхода остались выражения «возвести число в квадрат» или «в куб».

 

Различают следующие виды фигурных чисел:

·       Линейные числа — числа, не разлагающиеся на сомножители, то есть их ряд совпадает с рядом простых чисел, дополненным единицей:

1, 2, 3, 5, 7, 11, 13, 17, 19, 23, … (последовательность 

 

·       Плоские числа — числа, представимые в виде произведения двух сомножителей, то есть составные:

4, 6, 8, 9, 10, 12, 14, 15, … (последовательность 

 

·        Телесные числа — числа, представимые произведением трёх сомножителей:

8, 12, 16, 18, 20, 24, 27, 28, … (последовательность 

 

 

Многоугольные числа

 

·       Треугольные числа

 

Треугольное число — это число кружков, которые могут быть расставлены в форме равностороннего треугольника, см. рисунок. Очевидно, с чисто арифметической точки зрения, n-е треугольное число — это сумма n первых натуральных чисел.

 

 

 

 

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210 …, {\textstyle {\frac {n(n+1)}{2}}}

 

·       

Квадратные числа

 

{\displaystyle 0+\color {blue}1\color {black}=1}0+1 = 1	1               =3=4{\displaystyle 1+\color {blue}3\color {black}=4}	4=5=9{\displaystyle 4+\color {blue}5\color {black}=9}	9 =7=16{\displaystyle 9+\color {blue}7\color {black}=16}

 

Квадратные числа представляют собой произведение двух одинаковых натуральных чисел, то есть являются полными квадратами:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400 ,n²{\displaystyle n^{2}}

Каждое квадратное число, кроме единицы, есть сумма двух последовательных треугольных чисел

 

 

·       Пятиугольные числа

 

Последовательность пятиугольных чисел имеет вид:

1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590

n( 3n-1)/2…, {\textstyle {\frac {n(3n-1)}{2}}}

 

·       Шестиугольные числа

 

Шестиугольное число — фигурное число. n-ое шестиугольное число — число точек в состоящем из них правильном шестиугольнике со стороной в n точек.

 

          Шестиугольное число

 

 

 

1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, 630, 703, 780 …, {\displaystyle 2n^{2}-n}

2n² - n 

 

·       Восьмиугольные числа   3n² -2n

 

·       Двенадцатиугольные числа     5n² – 4n

1, 12, 33, 64, 105, 156, 217, 288, 369, 460, 561, 672, 793, 924, 1065, 1216, 1377, 1548, 1729, 1920

 

·        Плоские многоугольные числа — числа, связанные с определённым многоугольником. Они делятся на классические и центрированные.

·        Пространственные многогранные числа — числа, связанные с определённым многогранником.